جدول الضرب كامل وبالصور (من 1 حتى 20)

ليس فقط في امتحان الرياضيات والفيزياء، ولا يقتصر على الحسابات الهندسية… جدول الضرب جزء أساسي من حياتنا اليومية، في كل مرة تنظر إلى الساعة، وفي كل فاتورة مشتريات… في كل بناء ضخم وصناعة ناجحة… جدول الضرب له دور!
جدول الضرب Multiplication table هو قائمة خاصة بمضاعفات عدد، أو مخطط يجمع جداول الضرب الأساسية لمجموعة من الأعداد بحيث تشكل شبكة ويوفر الوقت والجهد في الوصول إلى حاصل ضرب عددين.
عملية الضرب Multiplication
الضرب من العمليات الحسابية الأساسية والتي تعرّف على أنها حاصل ضرب عددين أو أكثر، ويمكن تعريفها بشكل مبسط على أنها عملية الجمع المتكرر بين مجموعات ذات أحجام متساوية أي هي تمثل بشكل مجرد عملية الإضافة المتكررة لنفس العدد.
فإذا كان لديك 3 أكياس في كل كيس 4 تفاحات، عندها يمكنك الوصول إلى مجموع التفاح الكلي من خلال جمع 4 تفاحات لثلاث مرات 4 + 4 + 4 = 12 وهذا يقابل عملية الضرب 4 * 3 = 12 في المثال السابق قمنا بتبسيط عملية الجمع بالاعتماد على الضرب.
صيغة عملية الضرب

الأرقام الداخلة في عملية الضرب تسمى بالعوامل: العامل الأول يسمى المُضاعَفْ Multiplicand أي الرقم الذي نقوم بمضاعفته، والعامل الثاني يسمى المضاعِف Multiplier أي مقدار التضعيف، والنتيجة التي نحصل عليها تسمى حاصل ضرب هذه الأرقام Product.
على الرغم من هذه التسمية إلا أن الضرب عملية تبديلية، وبالتالي لا يهم ترتيب العوامل.
يرمز إلى عملية الضرب عادة بـ × أو النجمة * أو النقطة المتوسطة . كذلك فإن وضع الأقواس أو الرموز بجانب بعضها بدون إشارة تفصل بينها يعبر عن عملية الضرب، ويتم الاعتماد على أحد هذه الرموز حسب المادة العلمية وطبيعة العمليات الحسابية ومعناها الفيزيائي… بحيث لا يتم خلط إشارة الضرب بأي رمز آخر.
مع أخذ بعين الاعتبار أن في العمليات على المتجهات هناك فرق كبير في رمز الضرب المستخدم فالرمز × يعبر عن الجداء المتجهي ويكون الناتج في هذه الحالة شعاع (متجه) أما الرمز النقطة فهو يعبر عن الجداء السُلمي ويكون الناتج في هذه الحالة عدد.
ما هو جدول الضرب؟
يتم تعريف جدول الضرب بأنه جدول رياضي يستخدم لتحديد ناتج ضرب الأرقام الأساسية من 1 حتى 10، كذلك يمكن تمثيل الأرقام الأكبر ضمن جداول الضرب، حيث يتم ترتيبه وفق تسلسل منطقي.
يتم تمثيل عوامل الضرب في الصف والعمود الأول من جدول الضرب، بحيث يكون كل صف وعمود هو مضاعفات الرقم الأول فيه.
تاريخ جدول الضرب
يرجع استخدام جدول الضرب إلى العصور القديمة حيث تم استخدام الجداول لتمثيل العلاقة ما بين الأرقام وعملية الضرب…
على الرغم من أن مكتشف جدول الضرب غير معروف بدقة، ولكن اكتشاف جدول الضرب وتطوره قد مر بالمحطات التالية وساهمت مختلف الحضارات بوصوله إلى ما هو عليه اليوم:
حضارة البابلية ما بين النهرين القديمة
البداية كانت منذ أكثر من 4000 عام عند حضارة ما بين النهرين القديمة والتي تعتبر من أقدم الحضارات المعروفة، حيث قام البابليون بتطوير أنظمة رياضية واستخدام ألواح الطين لتمثيل وتسجيل العمليات الحسابية بما فيها جدول الضرب حيث احتوت هذه الألواح على جداول الضرب والقسمة…
حضارة مصر القديمة
استخدم المصريون القدماء الرموز الهيروغليفية لتمثيل الأرقام وإجراء العمليات الحسابية، حيث طوروا نظام ضرب خاص يسمى “طريقة الضرب المصرية“.
حضارة الصين القديمة
قام الصينيون القدماء بتطوير نظام رياضي يتضمن جداول الضرب، حيث تم تجميع جدول الضرب الصيني حوالي القرن الأول قبل الميلاد، وكان هذا الجدول عبارة عن مجموعة من المسائل الرياضية والحلول… وقد اشتمل على عمليات الضرب والقسمة.
العصر الإسلامي الذهبي
في العصر الإسلامي الذهبي وتحديدًا ما بين القرنين الثامن والرابع عشر الميلادي، تميز التقدم العلمي حيث حقق العلماء المسلمون تطورات مهمة في العلوم الرياضية، مثل: الخوارزمي، الكندي… وتضمنت هذه الإنجازات عمليات الضرب.
عصر النهضة والعصر الحديث
شهد عصر النهضة في أوروبا تقدم كبير في المعرفة الرياضية ولعب علماء ومبدعين مثل ليوناردو فيبوناتشي وسيمون ستيفين… دور في تطوير مفاهيم رياضية مهمة بما فيها الضرب. حيث قام فيبوناتشي بنشر الأرقام العربية ونظام الأرقام العشري في أوروبا، وعالم الرياضيات ستفين قام بنشر أعمال في الحساب وطور طرق للضرب والقسمة…
جدول الضرب الذي نعرفه اليوم، هو نتيجة لمساهمات مختلف الثقافات وجهود علماء الرياضيات!
جدول الضرب كامل
جدول الضرب أو مخطط جدول الضرب هو طريقة وأداة مفيدة لفهم الضرب والتعامل معه، يسمح بالوصول إلى نواتج عمليات الضرب الأساسية بسهولة وسرعة وأقل جهد ممكن.
جدول ضرب الأعداد من 1 إلى 10
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
جدول ضرب الأعداد من 11 إلى 20
| × | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 11 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
كيفية استخدام جدول الضرب
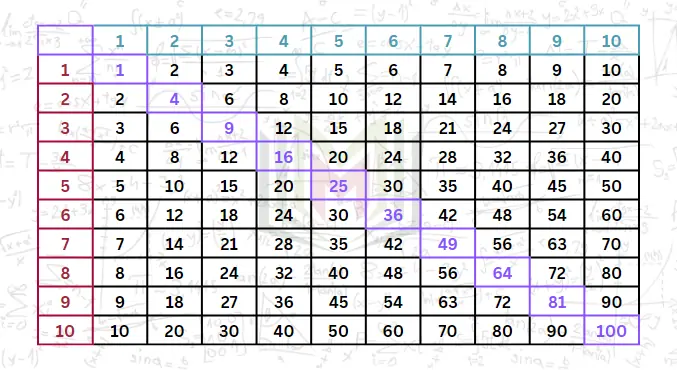
للحصول على ناتج عملية ضرب من جدول الضرب عليك مقاطعة الصف والعمود الخاص بالعوامل الداخلة في عملية الضرب.
مثال: 7 × 9 أي يجب النظر إلى صف 7 وعمود 9 والمربع الناتج عن مقاطعتهما يكون ناتج عملية الضرب وهو 63.
ملاحظات حول استخدام جدول الضرب
- مربع الأعداد: قطر جدول الضرب، يمثل مربعات الأعداد، لأنه تقاطع العدد مع نفسه، أي ناتج ضرب العدد بنفسه، وهذا يمثل مربعه.
- خاصية التبادلية: الضرب عملية تبديلية، وهذا الأمر ينطبق على جدول الضرب أيضًا، وبالتالي لا فرق في ترتيب العوامل سواء نظرت في عمود أو صف الأعداد الداخلة في الضرب، المهم أن تبحث عن تقاطع الأعداد الصحيح.
- تبعًا لخاصية التبادلية، فإن نواتج عمليات الضرب تكون متناظرة بالنسبة للقطر.
- امتداد الصف أو العمود يمثل مضاعفات العدد الأول في هذا الصف أو العمود، ومن خلالها يمكن الحصول على جدول الضرب الخاص بعدد محدد.
جدول الضرب كامل مكتوب (من الرقم 1 حتى 20)
جدول الضرب كامل للأعداد من 1 وحتى 5
| جدول الضرب للعدد 1 | جدول الضرب للعدد 2 | جدول الضرب للعدد 3 | جدول الضرب للعدد 4 | جدول الضرب للعدد 5 |
| 1 × 1 = 1 | 2 × 1 = 2 | 3 × 1 = 3 | 4 × 1 = 4 | 5 × 1 = 5 |
| 1 × 2 = 2 | 2 × 2 = 4 | 3 × 2 = 6 | 4 × 2 = 8 | 5 × 2 = 10 |
| 1 × 3 = 3 | 2 × 3 = 6 | 3 × 3 = 9 | 4 × 3 = 12 | 5 × 3 = 15 |
| 1 × 4 = 4 | 2 × 4 = 8 | 3 × 4 = 12 | 4 × 4 = 16 | 5 × 4 = 20 |
| 1 × 5 = 5 | 2 × 5 = 10 | 3 × 5 = 15 | 4 × 5 = 20 | 5 × 5 = 25 |
| 1 × 6 = 6 | 2 × 6 = 12 | 3 × 6 = 18 | 4 × 6 = 24 | 5 × 6 = 30 |
| 1 × 7 = 7 | 2 × 7 = 14 | 3 × 7 = 21 | 4 × 7 = 28 | 5 × 7 = 35 |
| 1 × 8 = 8 | 2 × 8 = 16 | 3 × 8 = 24 | 4 × 8 = 32 | 5 × 8 = 40 |
| 1 × 9 = 9 | 2 × 9 = 18 | 3 × 9 = 27 | 4 × 9 = 36 | 5 × 9 = 45 |
| 1 × 10 = 10 | 2 × 10 = 20 | 3 × 10 = 30 | 4 × 10 = 40 | 5 × 10 = 50 |
جدول الضرب للعدد 0
خاصية الصفر في عملية الضرب تتمثل بكونه عامل يجعل ناتج الضرب دائمًا صفر مهما كان، أي أن حاصل ضرب أي عدد بـ صفر هو 0.
مثال: 0 × 9 = 0
جدول الضرب للعدد 1
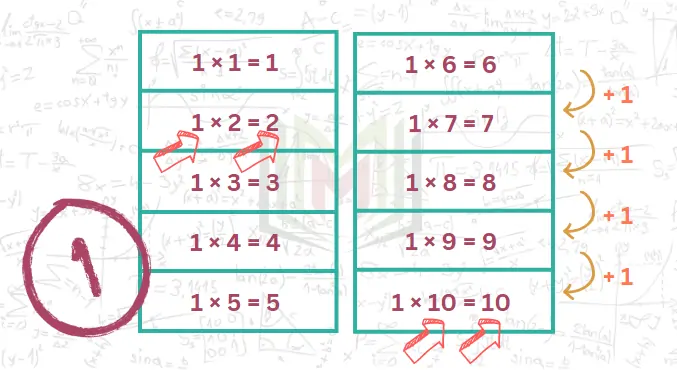
في عملية الضرب يعتبر العدد 1 هو العامل الحيادي، فناتج ضرب أي عدد بـ 1 يعطي العدد نفسه.
مثال: 1 × 9 = 9
جدول الضرب للعدد 2

جدول ضرب 2 أو مضاعفات العدد 2، من الجداول الأساسية سهل الحفظ، تتميز بـ:
- تتبع نمط 0 2 4 6 8 في خانة الآحاد.
- ناتج ضرب أي عدد بـ 2 يكون عدد زوجي دائمًا.
مثال: 7 × 2 = 14 (14 عدد زوجي)
جدول الضرب للعدد 3
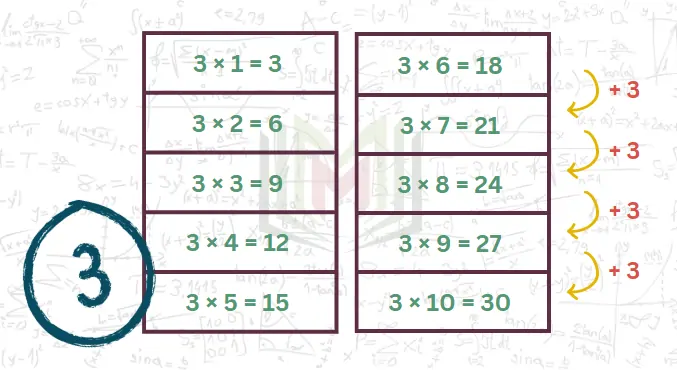
جدول ضرب 3 أو مضاعفات العدد 3، وهو جدول ضرب للعدد الأولي الأول 3، ويعد تعلمه مهارة أساسية في الحساب.
هذا الجدول لا يتبع أي نمط ثابت، ولكنه يتميز بأن حاصل جمع أرقام الناتج دائمًا هو عدد يقبل القسمة على 3.
مثال: 4 × 3 = 12 (12 وبالتالي 2 + 1 = 3 وهو يقبل القسمة على 3)
جدول الضرب للعدد 4

جدول الضرب لـ 4 أو مضاعفات العدد 4، يعتبر جدول مشابه لجدول العدد 2، جميع نواتج الضرب بـ 4 هي أعداد زوجية، ولكنه لا يتبع نمطًا ثابتا إلا لكل عشر نواتج.
مثال: 2 × 4 = 8 (8 عدد زوجي)
جدول الضرب للعدد 5

يتمتع جدول مضاعفات العدد 5 بميزة فريدة حيث أن ناتج الضرب دائمًا ينتهي إما بـ 0 أو 5 (منزلة الآحاد)، مهما كان عدد مرات مضاعفة الـ 5.
مثال: 9 × 5 = 45 (45 آحاده 5)، 10 × 5 = 50 (50 آحاده 0)
جدول الضرب كامل للأعداد من 6 إلى 10
| جدول الضرب للعدد 6 | جدول الضرب للعدد 7 | جدول الضرب للعدد 8 | جدول الضرب للعدد 9 | جدول الضرب للعدد 10 |
| 6 × 1 = 6 | 7 × 1 = 7 | 8 × 1 = 8 | 9 × 1 = 9 | 10 × 1 = 10 |
| 6 × 2 = 12 | 7 × 2 = 14 | 8 × 2 = 16 | 9 × 2 = 18 | 10 × 2 = 20 |
| 6 × 3 = 18 | 7 × 3 = 21 | 8 × 3 = 24 | 9 × 3 = 27 | 10 × 3 = 30 |
| 6 × 4 = 24 | 7 × 4 = 28 | 8 × 4 = 32 | 9 × 4 = 36 | 10 × 4 = 40 |
| 6 × 5 = 30 | 7 × 5 = 35 | 8 × 5 = 40 | 9 × 5 = 45 | 10 × 5 = 50 |
| 6 × 6 = 36 | 7 × 6 = 42 | 8 × 6 = 48 | 9 × 6 = 54 | 10 × 6 = 60 |
| 6 × 7 = 42 | 7 × 7 = 49 | 8 × 7 = 56 | 9 × 7 = 63 | 10 × 7 = 70 |
| 6 × 8 = 48 | 7 × 8 = 56 | 8 × 8 = 64 | 9 × 8 = 72 | 10 × 8 = 80 |
| 6 × 9 = 54 | 7 × 9 = 63 | 8 × 9 = 72 | 9 × 9 = 81 | 10 × 9 = 90 |
| 6 × 10 = 60 | 7 × 10 = 70 | 8 × 10 = 80 | 9 × 10 = 90 | 10 × 10 = 100 |
جدول الضرب للعدد 6

مضاعفات العدد 6 هي مضاعفات كل من العددين 2 و3 معًا، في وقت واحد، كذلك فإن ناتج ضرب أي عدد بـ 6 هو عدد زوجي.
مثال: 4 × 6 = 24 (24 عدد زوجي وهو من مضاعفات الـ 2 حيث 2 × 12 = 24، وكذلك من مضاعفات العدد 3 حيث 8 × 3 = 24)
جدول الضرب للعدد 7
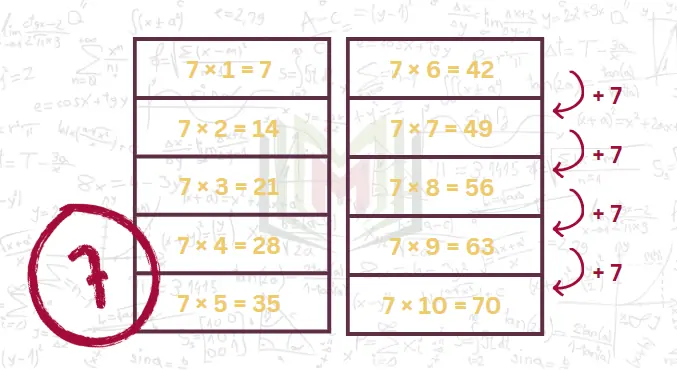
العدد 7 هو عدد أولي، ونواتج مضاعفاته لا تتبع نمط ثابت، كذلك فهو يتميز بأن الـ 7 لا تظهر في جدول ضرب الـ 7 قبل العدد 10.
مثال: 10 × 7 = 70
جدول الضرب للعدد 8

مضاعفات العدد 8 تتبع نمط آحاد يتكرر كل 5 مضاعفات وهو: 8 6 4 2 0 ونواتج الضرب دائمًا أعداد زوجية، يمكن حفظه من خلال فهم علاقة المضاعفات ببعضها أو حفظه بطريقة تخطي العد، ومن الجدير بالذكر أن حفظ جدول ضرب 8 سوف يزيد من مهارة وسرعة وسهولة حل المشكلات الرياضية والحسابية.
مثال: 9 × 8 = 72 (72 عدد زوجي)
جدول الضرب للعدد 9
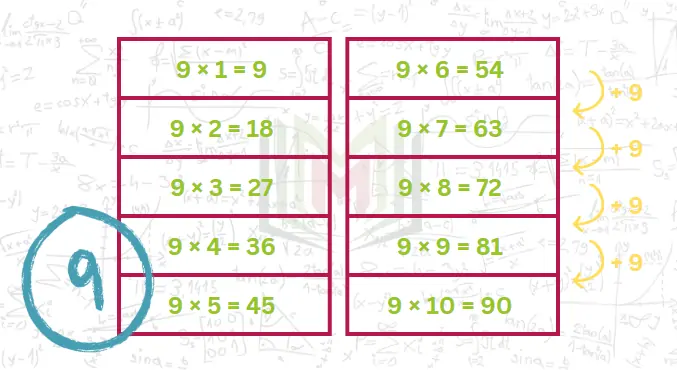
مضاعفات العدد 9 تتبع نمط سهل يتمثل في أن الآحاد تتناقص من 9 حتى 0 والعشرات تتزايد من 0 وحتى 9 (التناقص والتزايد يكون بمقدار 1).
مثال: 1 × 9 = 9 وبعده 2 × 9 = 18 (لاحظ الناتج الأول هو 09 أحاده 9 وعشراته 0 والناتج التالي هو 18 أحداه 8 وعشراته 1، وهكذا تتناقص الآحاد بمقدار 1 وتتزايد العشرات بمقدار 1)
جدول الضرب للعدد 10

جدول مضاعفات العدد 10 يعتبر من أسهل الجداول، فيمكن الوصول إلى ناتج ضرب أي عدد بـ 10 من خلال إضافة 0 بعد الرقم (أي زيادة مرتبة العدد نفسه).
مثال: 1 × 10 = 100
جدول الضرب كامل للأرقام من 11 وحتى 15
| جدول الضرب للعدد 11 | جدول الضرب للعدد 12 | جدول الضرب للعدد 13 | جدول الضرب للعدد 14 | جدول الضرب للعدد 15 |
| 11 × 1 = 11 | 12 × 1 = 12 | 13 × 1 = 13 | 14 × 1 = 14 | 15 × 1 = 15 |
| 11 × 2 = 22 | 12 × 2 = 24 | 13 × 2 = 26 | 14 × 2 = 28 | 15 × 2 = 30 |
| 11 × 3 = 33 | 12 × 3 = 36 | 13 × 3 = 39 | 14 × 3 = 42 | 15 × 3 = 45 |
| 11 × 4 = 44 | 12 × 4 = 48 | 13 × 4 = 52 | 14 × 4 = 56 | 15 × 4 = 60 |
| 11 × 5 = 55 | 12 × 5 = 60 | 13 × 5 = 65 | 14 × 5 = 70 | 15 × 5 = 75 |
| 11 × 6 = 66 | 12 × 6 = 72 | 13 × 6 = 78 | 14 × 6 = 84 | 15 × 6 = 90 |
| 11 × 7 = 77 | 12 × 7 = 84 | 13 × 7 = 91 | 14 × 7 = 98 | 15 × 7 = 105 |
| 11 × 8 = 88 | 12 × 8 = 96 | 13 × 8 = 104 | 14 × 8 = 112 | 15 × 8 = 120 |
| 11 × 9 = 99 | 12 × 9 = 108 | 13 × 9 = 117 | 14 × 9 = 126 | 15 × 9 = 135 |
| 11 × 10 = 110 | 12 × 10 = 120 | 13 × 10 = 130 | 14 × 10 = 140 | 15 × 10 = 150 |
جدول الضرب للعدد 11

يمكن الحصول على ناتج ضرف أي عدد مكون من خانة واحدة بـ 11 من خلال تكرار كتابة العدد مرتين، أما بالنسبة للأعداد المكونة من خانتين فعليك مباعدة الخانتين وكتابة مجموعهما في الوسط.
مثال: 2 × 11 = 22 (أي 22 من كتابة 2 مرتين)، أما 12 × 11 = 132 (أي قمنا بمباعدة الـ 2 عن 1 وكتابة 3 الناتجة عن مجموعة خانتي 12)
جدول الضرب للعدد 12

جدول مضاعفات العدد 12 يتميز بالنمط 2 4 6 8 0 في خانة الآحاد يتكرر كل 5 مضاعفات، أي أن الناتج دائمًا زوجي.
مثال: 3 × 12 = 36
جدول الضرب للعدد 13

لا يوجد نمط يميز مضاعفات العدد 13، ولكن في المقابل يمكن الوصول إلى الناتج بالاعتماد على مضاعفات العدد 3 والعدد 10 معًا.
مثال: 5 × 13 = 65 (حيث 5 × 3 = 15 أي 5 في الآحاد و1 في العشرات، و5 × 10 = 50 ولا تنسى وجود 1 إضافي في العشرات هذا يجعل الجواب النهائي 65)
جدول الضرب للعدد 14

جدول مضاعفات العدد 14 يتبع نمط 4 8 2 6 0 يتكرر كل 5 مضاعفات، وبطريقة مشابهة لجداول ضرب 12 و13 يمكن الحصول على ناتج ضرب أي عدد بـ 14 بالاعتماد على جدول ضرب 4 وجدول ضرب 10.
مثال: 5 × 14 = 70 (حيث 5 × 4 = 20 أي 0 في الآحاد و2 في العشرات، و5 × 10 = 50 ولا تنسى وجود 2 إضافية في العشرات هذا يجعل الجواب النهائي 70)
جدول الضرب للعدد 15

بشكل مشابه لجدول ضرب 5 فإن مضاعفات العدد 15 أيضًا تنتهي إما بـ 5 أو 0، وبطريقة مشابهة لجداول الضرب الأكبر من 10 يتم الحصول على الناتج بالاعتماد على جدولي الـ 5 والـ 10 معًا.
مثال: 5 × 15 = 75 (حيث 5 × 5 = 25 أي 5 في الآحاد و2 في العشرات، و5 × 10 = 50 ولا تنسى وجود 2 إضافية في العشرات هذا يجعل الجواب النهائي 75)
جدول الضرب كامل للأرقام من 16 وحتى 20
| جدول الضرب للعدد 16 | جدول الضرب للعدد 17 | جدول الضرب للعدد 18 | جدول الضرب للعدد 19 | جدول الضرب للعدد 20 |
| 16 × 1 = 16 | 17 × 1 = 17 | 18 × 1 = 18 | 19 × 1 = 19 | 20 × 1 = 20 |
| 16 × 2 = 32 | 17 × 2 = 34 | 18 × 2 = 36 | 19 × 2 = 38 | 20 × 2 = 40 |
| 16 × 3 = 48 | 17 × 3 = 51 | 18 × 3 = 54 | 19 × 3 = 57 | 20 × 3 = 60 |
| 16 × 4 = 64 | 17 × 4 = 68 | 18 × 4 = 72 | 19 × 4 = 76 | 20 × 4 = 80 |
| 16 × 5 = 80 | 17 × 5 = 85 | 18 × 5 = 90 | 19 × 5 = 95 | 20 × 5 = 100 |
| 16 × 6 = 96 | 17 × 6 = 102 | 18 × 6 = 108 | 19 × 6 = 114 | 20 × 6 = 120 |
| 16 × 7 = 112 | 17 × 7 = 119 | 18 × 7 = 126 | 19 × 7 = 133 | 20 × 7 = 140 |
| 16 × 8 = 128 | 17 × 8 = 136 | 18 × 8 = 144 | 19 × 8 = 152 | 20 × 8 = 160 |
| 16 × 9 = 144 | 17 × 9 = 153 | 18 × 9 = 162 | 19 × 9 = 171 | 20 × 9 = 180 |
| 16 × 10 = 160 | 17 × 10 = 170 | 18 × 10 = 180 | 19 × 10 = 190 | 20 × 10 = 200 |
جدول الضرب للعدد 16
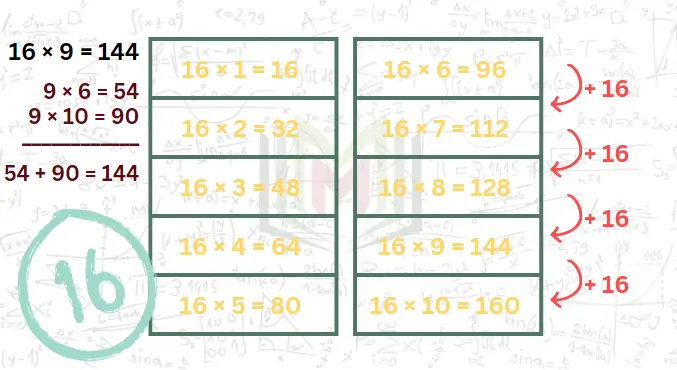
كما هو الحال مع جداول الضرب السابقة، يمكنك الوصول إلى مضاعفات العدد 16 بالاعتماد على جداول الضرب الأساسية 6 و10.
مثال: 9 × 16 = 144 (حيث 9 × 6 = 54 أي 4 في الآحاد و5 في العشرات، و9 × 10 = 90 ولا تنسى وجود 5 إضافية في العشرات هذا يجعل الجواب النهائي 144)
جدول الضرب للعدد 17

أسهل طريقة لحفظ مضاعفات العدد 17 هي الاعتماد على جدول ضرب 7 وجدول ضرب 10.
مثال: 8 × 17 = 136 (حيث 8 × 7 = 56 أي 6 في الآحاد و5 في العشرات، و8 × 10 = 80 ولا تنسى وجود 5 إضافية في العشرات هذا يجعل الجواب النهائي 136)
جدول الضرب للعدد 18

يتبع جدول ضرب 18 نمط 8 6 4 2 0 في الآحاد يتكرر كل 5 مضاعفات، ويمكن بسهولة معرفة مضاعفات العدد 18 بالاعتماد على جدولي 8 و10.
مثال: 7 × 18 = 126 (حيث 7 × 8 = 56 أي 6 في الآحاد و5 في العشرات، و7 × 10 = 70 ولا تنسى وجود 5 إضافية في العشرات هذا يجعل الجواب النهائي 126)
جدول الضرب للعدد 19

يتميز جدول ضرب 19 بأن مرتبة الآحاد تتناقص بمقدار 1 بداية من 9 وحتى 0، وخانة العشرات تتزايد بمقدار 2 بداية من 1 وحتى 9 ومن ثم تعود لـ 1 وتكرر التزايد بمقدار 2 وهكذا… أيضًا يتم الاعتماد على جداول 9 و10.
مثال: 8 × 19 = 152 (حيث 8 × 9 = 72 أي 2 في الآحاد و7 في العشرات، و8 × 10 = 80 ولا تنسى وجود 7 إضافية في العشرات هذا يجعل الجواب النهائي 152)
جدول الضرب للعدد 20

بطريقة مشابهة لجدول ضرب 10، ولكن هذه المرة مع مضاعفة الناتج، أي ضع صفر بجانب العدد وضاعفه مرة.
مثال: 4 × 20 = 80
جدول الضرب وجداول مضاعفات الأعداد… إنها جزء أساسي من حياتنا، ولكن هل بالفعل تحتاج لحفظها بطريقة صعبة ومملة؟ الجواب لا، لأنك ستعتمد على أسهل طريقة لحفظ جدول الضرب.
المصادر





